Alpha compositing

From Wikipedia, the free encyclopedia

Jump to navigation Jump to search

It has been suggested that this article be merged with Alpha mapping. (Discuss) Proposed since November 2019.

This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed. Find sources: "Alpha compositing" – news · newspapers · books · scholar · JSTOR (May 2010) (Learn how and when to remove this template message)

This color spectrum image's alpha channel falls off to zero at its base, where it is blended with the background color.

In computer graphics, alpha compositing is the process of combining one image with a background to create the appearance of partial or full transparency. It is often useful to render picture elements (pixels) in separate passes or layers and then combine the resulting 2D images into a single, final image called the composite. Compositing is used extensively in film when combining computer-rendered image elements with live footage. Alpha blending is also used in 2D computer graphics to put rasterized foreground elements over a background.

In order to combine the picture elements of the images correctly, it is necessary to keep an associated matte for each element in addition to its color. This matte layer contains the coverage information—the shape of the geometry being drawn—making it possible to distinguish between parts of the image where something was drawn and parts that are empty.

Although the most basic operation of combining two images is to put one over the other, there are many operations, or blend modes, that are used.

Contents

• 1 Description
  • 1.1 Straight versus premultiplied
  • 1.2 Examples of different operations
• 2 Analytical derivation of the over operator
• 3 Alpha blending
• 4 Other transparency methods
• 5 Composing alpha blending with gamma correction
• 6 See also
• 7 References
• 8 External links

Description[edit]

To store matte information, the concept of an alpha channel was introduced by Alvy Ray Smith in the late 1970s and fully developed in a 1984 paper by Thomas Porter and Tom Duff.^[1] In a 2D picture element (pixel), which stores a color for each pixel, additional data is stored in the alpha channel with a value ranging from 0 to 1. A value of 0 means that the pixel is transparent and does not provide any coverage information; i.e. there is no occlusion at the image pixel window because the geometry did not overlap this pixel. A value of 1 means that the pixel is fully occluding because the geometry completely overlaps the pixel window.

Straight versus premultiplied[edit]

If an alpha channel is used in an image, there are two common representations that are available: straight (unassociated) alpha, and premultiplied (associated) alpha.

With straight alpha, the RGB components represent the color of the object or pixel, disregarding its opacity.

With premultiplied alpha, the RGB components represent the emission of the object or pixel, and the alpha represents the occlusion. A more obvious advantage of this is that, in certain situations, it can save a subsequent multiplication (e.g. if the image is used many times during later compositing). However, the most significant advantages of using premultiplied alpha are for correctness and simplicity rather than performance: premultiplied alpha allows correct filtering and blending. In addition, premultiplied alpha allows regions of regular alpha blending and regions with additive blending mode to be encoded within the same image, because channel values are usually stored in a fixed-point format which bounds the values to be between 0 and 1.^[2]

Assuming that the pixel color is expressed using straight (non-premultiplied) RGBA tuples, a pixel value of (0, 0.7, 0, 0.5) implies a pixel that has 70% of the maximum green intensity and 50% opacity. If the color were fully green, its RGBA would be (0, 1, 0, 0.5).

However, if this pixel uses premultiplied alpha, all of the RGB values (0, 0.7, 0) are multiplied, or scaled for occlusion, by the alpha value 0.5, which is appended to yield (0, 0.35, 0, 0.5). In this case, the 0.35 value for the G channel actually indicates 70% green emission intensity (with 50% occlusion). A pure green emission would be encoded as (0, 0.5, 0, 0.5). Knowing whether a file uses straight or premultiplied alpha is essential to correctly process or composite it, as a different calculation is required. It is also entirely acceptable to have an RGBA triplet express emission with no occlusion, such as (0.4, 0.3, 0.2, 0.0). Fires and flames, glows, flares, and other such phenomena can only be represented using associated / premultiplied alpha.

The only important difference is in the dynamic range of the colour representation in finite precision numerical calculations (which is in all applications): premultiplied alpha has a unique representation for transparent pixels, avoiding the need to choose a "clear color" or resultant artifacts such as edge fringes (see the next paragraphs). In an associated / premultiplied alpha image, the RGB represents the emission amount, while the alpha is occlusion. Premultiplied alpha has some practical advantages over normal alpha blending because interpolation and filtering give correct results.^[3]

Ordinary interpolation without premultiplied alpha leads to RGB information leaking out of fully transparent (A=0) regions, even though this RGB information is ideally invisible. When interpolating or filtering images with abrupt borders between transparent and opaque regions, this can result in borders of colors that were not visible in the original image. Errors also occur in areas of semitransparency because the RGB components are not correctly weighted, giving incorrectly high weighting to the color of the more transparent (lower alpha) pixels.

Premultiplication can reduce the available relative precision in the RGB values when using integer or fixed-point representation for the color components, which may cause a noticeable loss of quality if the color information is later brightened or if the alpha channel is removed. In practice, this is not usually noticeable because during typical composition operations, such as OVER, the influence of the low-precision colour information in low-alpha areas on the final output image (after composition) is correspondingly reduced. This loss of precision also makes premultiplied images easier to compress using certain compression schemes, as they do not record the color variations hidden inside transparent regions, and can allocate fewer bits to encode low-alpha areas. The same "limitations" of lower quantisation bit depths such as 8 bit per channel are also present in imagery without alpha, and this argument is problematic as a result.

With the existence of an alpha channel, it is possible to express compositing image operations using a compositing algebra. For example, given two image elements A and B, the most common compositing operation is to combine the images such that A appears in the foreground and B appears in the background. This can be expressed as A over B. In addition to over, Porter and Duff defined the compositing operators in, held out by (usually abbreviated out), atop, and xor (and the reverse operators rover, rin, rout, and ratop) from a consideration of choices in blending the colors of two pixels when their coverage is, conceptually, overlaid orthogonally:

The over operator is, in effect, the normal painting operation (see Painter's algorithm). The in operator is the alpha compositing equivalent of clipping.

As an example, the over operator can be accomplished by applying the following formula to each pixel value:

${\displaystyle C_{o}={\frac {C_{a}\alpha _{a}+C_{b}\alpha _{b}(1-\alpha _{a})}{\alpha _{a}+\alpha _{b}(1-\alpha _{a})}}}$

where ${\displaystyle C_{o}}$ is the result of the operation, ${\displaystyle C_{a}}$ is the color of the pixel in element A, ${\displaystyle C_{b}}$ is the color of the pixel in element B, and ${\displaystyle \alpha _{a}}$ and ${\displaystyle \alpha _{b}}$ are the alpha of the pixels in elements A and B respectively. If it is assumed that all color values are premultiplied by their alpha values (${\displaystyle c_{i}=\alpha _{i}C_{i}}$), we can rewrite the equation for output color as:

${\displaystyle c_{o}=c_{a}+c_{b}(1-\alpha _{a})}$

and resulting alpha channel value is

${\displaystyle \alpha _{o}={\frac {c_{o}}{C_{o}}}=\alpha _{a}+\alpha _{b}(1-\alpha _{a})}$

Examples of different operations[edit]

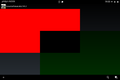
Examples of red overlaid with green, with both colours fully opaque:

• 

  ADD operation

• 

  CLEAR operation

• 

  MULTIPLY operation

• 

  OVERLAY operation

Analytical derivation of the over operator[edit]

Porter and Duff gave a geometric interpretation of the alpha compositing formula by studying orthogonal coverages. Another derivation of the formula, based on a physical reflectance/transmittance model, can be found in a 1981 paper by Bruce A. Wallace.^[4]

A third approach is found by starting out with two very simple assumptions. For simplicity, we shall here use the shorthand notation ${\displaystyle a\odot b}$ for representing the over operator.

The first assumption is that in the case where the background is opaque (i.e. ${\displaystyle \alpha _{b}=1}$), the over operator represents the convex combination of ${\displaystyle a}$ and ${\displaystyle b}$:

${\displaystyle C_{o}=\alpha _{a}C_{a}+(1-\alpha _{a})C_{b}}$

The second assumption is that the operator must respect the associative rule:

${\displaystyle (a\odot b)\odot c=a\odot (b\odot c)}$

Now, let us assume that ${\displaystyle a}$ and ${\displaystyle b}$ have variable transparencies, whereas ${\displaystyle c}$ is opaque. We're interested in finding

${\displaystyle o=a\odot b.}$

We know from the associative rule that the following must be true:

${\displaystyle o\odot c=a\odot (b\odot c)}$

We know that ${\displaystyle c}$ is opaque and thus follows that ${\displaystyle b\odot c}$ is opaque, so in the above equation, each ${\displaystyle \odot }$ operator can be written as a convex combination:

${\displaystyle {\begin{aligned}\alpha _{o}C_{o}+(1-\alpha _{o})C_{c}&=\alpha _{a}C_{a}+(1-\alpha _{a})(\alpha _{b}C_{b}+(1-\alpha _{b})C_{c})\\[5pt]&=[\alpha _{a}C_{a}+(1-\alpha _{a})\alpha _{b}C_{b}]+(1-\alpha _{a})(1-\alpha _{b})C_{c}\end{aligned}}}$

Hence we see that this represents an equation of the form ${\displaystyle X_{0}+Y_{0}C_{c}=X_{1}+Y_{1}C_{c}}$. By setting ${\displaystyle X_{0}=X_{1}}$ and ${\displaystyle Y_{0}=Y_{1}}$ we get

${\displaystyle {\begin{aligned}\alpha _{o}&=1-(1-\alpha _{a})(1-\alpha _{b}),\\[5pt]C_{o}&={\frac {\alpha _{a}C_{a}+(1-\alpha _{a})\alpha _{b}C_{b}}{\alpha _{o}}},\end{aligned}}}$

which means that we have analytically derived a formula for the output alpha and the output color of ${\displaystyle a\odot b}$.

An even more compact representation is given by noticing that ${\displaystyle (1-\alpha _{a})\alpha _{b}=\alpha _{o}-\alpha _{a}}$:

${\displaystyle C_{o}={\frac {\alpha _{a}}{\alpha _{o}}}C_{a}+\left(1-{\frac {\alpha _{a}}{\alpha _{o}}}\right)C_{b}}$

The ${\displaystyle \odot }$ operator fulfills all the requirements of a non-commutative monoid, where the identity element ${\displaystyle e}$ is chosen such that ${\displaystyle e\odot a=a\odot e=a}$ (i.e. the identity element can be any tuple ${\displaystyle \langle C,\alpha \rangle }$ with ${\displaystyle \alpha =0}$).

Alpha blending[edit]

Alpha blending is the process of combining a translucent foreground color with a background color, thereby producing a new color blended between the two. The degree of the foreground color's translucency may range from completely transparent to completely opaque. If the foreground color is completely transparent, the blended color will be the background color. Conversely, if it is completely opaque, the blended color will be the foreground color. The translucency can range between these extremes, in which case the blended color is computed as a weighted average of the foreground and background colors.

Alpha blending is a convex combination of two colors allowing for transparency effects in computer graphics. The value of alpha in the color code ranges from 0.0 to 1.0, where 0.0 represents a fully transparent color, and 1.0 represents a fully opaque color. This alpha value also corresponds to the ratio of "SRC over DST" in Porter and Duff equations.

The value of the resulting color is given by:

${\displaystyle {\begin{cases}\mathrm {out} _{A}=\mathrm {src} _{A}+\mathrm {dst} _{A}(1-\mathrm {src} _{A})\\\mathrm {out} _{\text{RGB}}={\bigl (}\mathrm {src} _{\text{RGB}}\mathrm {src} _{A}+\mathrm {dst} _{\text{RGB}}\mathrm {dst} _{A}\left(1-\mathrm {src} _{A}\right){\bigr )}\div \mathrm {out} _{A}\\\mathrm {out} _{A}=0\Rightarrow \mathrm {out} _{\text{RGB}}=0\end{cases}}}$

If the destination background is opaque, then ${\displaystyle {\text{dst}}_{A}=1}$, and if you enter it to the upper equation:

${\displaystyle {\begin{cases}\mathrm {out} _{A}=1\\\mathrm {out} _{\text{RGB}}=\mathrm {src} _{\text{RGB}}\mathrm {src} _{A}+\mathrm {dst} _{\text{RGB}}(1-\mathrm {src} _{A})\end{cases}}}$

The alpha component may be used to blend to red, green and blue components equally, as in 32-bit RGBA, or, alternatively, there may be three alpha values specified corresponding to each of the primary colors for spectral color filtering.

If premultiplied alpha is used, the above equations are simplified to:

${\displaystyle {\begin{cases}\mathrm {out} _{A}=\mathrm {src} _{A}+\mathrm {dst} _{A}(1-\mathrm {src} _{A})\\\mathrm {out} _{\text{RGB}}=\mathrm {src} _{\text{RGB}}+\mathrm {dst} _{\text{RGB}}\left(1-\mathrm {src} _{A}\right)\end{cases}}}$

Other transparency methods[edit]

Although used for similar purposes, transparent colors and image masks do not permit the smooth blending of the superimposed image pixels with those of the background (only whole image pixels or whole background pixels allowed).

A similar effect can be achieved with a 1-bit alpha channel, as found in the 16-bit RGBA Highcolor mode of the Truevision TGA image file format and related TARGA and AT-Vista/NU-Vista display adapters' Highcolor graphic mode. This mode devotes 5 bits for every primary RGB color (15-bit RGB) plus a remaining bit as the "alpha channel".

Composing alpha blending with gamma correction[edit]

Alpha blending, not taking into account the gamma correction

Alpha blending, taking into account the gamma correction. A demonstration with python code can be found here

The RGB values stored in computer images are actually not the real light intensities, but they have been transformed by a gamma correction, in order to optimize the usage of bits when encoding an image.

The gamma correction can be roughly summarised as below:

• let ${\displaystyle {\text{displayed}}_{\text{RGB}}}$ be the RGB intensity that is displayed on the screen (in normalised intensities, i.e. between 0 and 1)
• let ${\displaystyle {\text{stored}}_{\text{RGB}}}$ be the RGB intensity that is stored as bits in the computer memory (in normalised intensities also)
• let ${\displaystyle \gamma }$ be the "decoding" gamma of 2.2 of the ${\displaystyle {\text{stored}}_{\text{RGB}}}$ image (${\displaystyle \gamma }$ has a typical value of 2.2)

Then we have the following relation:

${\displaystyle {\text{displayed}}_{\text{RGB}}={\text{stored}}_{\text{RGB}}^{\gamma }}$

Thus, when dealing with computer stored RGB values, alpha blending will look much better if the gamma correction is unapplied before averaging the images and re-applied afterwards.^[5]

For example, if one wants to superimpose an image named ${\displaystyle overlay_{\text{rgb}}}$ with an alpha channel ${\displaystyle overlay_{\alpha }}$ onto a background image ${\displaystyle background_{\text{rgb}}}$, then the resulting image ${\displaystyle out_{\text{rgb}}}$ can be calculated like this:

${\displaystyle {\text{out}}_{\text{rgb}}=({\text{overlay}}_{\text{rgb}}^{\gamma }\times {\text{overlay}}_{\alpha }+{\text{background}}_{\text{rgb}}^{\gamma }\times (1-{\text{overlay}}_{\alpha }))^{1/\gamma }}$

Note: ${\displaystyle {\text{out}}_{\text{rgb}}}$ is the image as it will be stored in the computer memory; and it will be displayed as ${\displaystyle {\text{out}}_{\text{rgb}}^{\gamma }}$ on the computer display.

See also[edit]

• Alpha to coverage
• Bit blit
• Blend modes
• Digital compositing
• Image masks
• Magic Pink
• Portable Network Graphics
• RGBA color space
• Texture splatting
• Transparency (graphic)
• Transparent color in palettes
• Truevision TGA

References[edit]

1. ^ Porter, Thomas; Duff, Tom (July 1984). "Compositing Digital Images" (PDF). SIGGRAPH Computer Graphics. New York City, New York: ACM Press. 18 (3): 253–259. doi:10.1145/800031.808606. ISBN 9780897911382. Archived (PDF) from the original on 2011-04-29. Retrieved 2019-03-11.
2. ^ "TomF's Tech Blog - It's only pretending to be a wiki". tomforsyth1000.github.io. Archived from the original on 12 December 2017. Retrieved 8 May 2018.
3. ^ "ALPHA COMPOSITING – Animationmet". animationmet.com. Retrieved 2019-09-25.
4. ^ Wallace, Bruce A. (1981). "Merging and transformation of raster images for cartoon animation". SIGGRAPH Computer Graphics. New York City, New York: ACM Press. 15 (3): 253–262. CiteSeerX 10.1.1.141.7875. doi:10.1145/800224.806813. ISBN 0-89791-045-1.
5. ^ Minute Physics (March 20, 2015). "Computer Color is Broken". YouTube.

External links[edit]

• Compositing Digital Images - Thomas Porter and Tom Duff (Original Paper)
• Image Compositing Fundamentals
• Understand Compositing and Color extensions in SVG 1.2 in 30 minutes!
• Alpha Matting and Premultiplication

Retrieved from "https://en.wikipedia.org/w/index.php?title=Alpha_compositing&oldid=931486689"

Categories:

• Computer graphics algorithms

Hidden categories:

• Articles to be merged from November 2019
• All articles to be merged
• Articles needing additional references from May 2010
• All articles needing additional references

Navigation menu

Personal tools

• Not logged in
• Talk
• Contributions
• Create account
• Log in

Namespaces

• Article
• Talk

Variants

Views

• Read
• Edit
• View history

More

Search

Navigation

• Main page
• Contents
• Featured content
• Current events
• Random article
• Donate to Wikipedia
• Wikipedia store

Interaction

• Help
• About Wikipedia
• Community portal
• Recent changes
• Contact page

Tools

• What links here
• Related changes
• Upload file
• Special pages
• Permanent link
• Page information
• Wikidata item
• Cite this page

Print/export

• Create a book
• Download as PDF
• Printable version

Languages

• العربية
• Български
• Deutsch
• Español
• Français
• 한국어
• 日本語
• Українська
• 中文

Edit links

• This page was last edited on 19 December 2019, at 04:35 (UTC).
• Text is available under the Creative Commons Attribution-ShareAlike License; additional terms may apply. By using this site, you agree to the Terms of Use and Privacy Policy. Wikipedia® is a registered trademark of the Wikimedia Foundation, Inc., a non-profit organization.

• Privacy policy
• About Wikipedia
• Disclaimers
• Contact Wikipedia
• Developers
• Statistics
• Cookie statement
• Mobile view

• 
•